Appearance
题目
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
**注意:**答案中不可以包含重复的三元组。
示例
示例 1:
**输入:**nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]] 解释: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。
示例 2:
**输入:**nums = [0,1,1] 输出:[] **解释:**唯一可能的三元组和不为 0 。
示例 3:
**输入:**nums = [0,0,0] 输出:[[0,0,0]] **解释:**唯一可能的三元组和为 0 。
提示
3 <= nums.length <= 3000-105 <= nums[i] <= 105
代码-个人
java
public static List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
Arrays.sort(nums);
for(int i=0;i<nums.length-1;i++){
// 如果当前值大于0,后面的数都大于0,不可能相加为0
if(nums[i] > 0) return result;
// 去重
if(i > 0 && nums[i] == nums[i-1]) continue;
// 如果i+j+k>0,说明k太大了,k--
int left = i+1;
int right = nums.length - 1;
while(left < right) {
int sum = nums[i] + nums[left] + nums[right];
if(sum > 0) {
right--;
}else if(sum < 0) {
left++;
}else {
result.add(Arrays.asList(nums[i], nums[left], nums[right]));
// 去重
while(left < right && nums[left] == nums[left+1]) left++;
while(left < right && nums[right] == nums[right-1]) right--;
left++;
right--;
}
}
}
return result;
}官方题解
先对数组排序,设一非递减的数组示例和初始三指针位置及名字如下所示。 固定i,即可转换为寻找满足 num**s[l]+num**s[r]=−num**s[i] 的三元组,借用两数之和的思路即可。
固定i,即可转换为寻找满足 num**s[l]+num**s[r]=−num**s[i] 的三元组,借用两数之和的思路即可。
还要注意因为不能包含重复的三元组,以下两个三元组只能取一个,而后我们再考虑其是否满足 num**s[l]+num**s[r]=−num**s[i]。
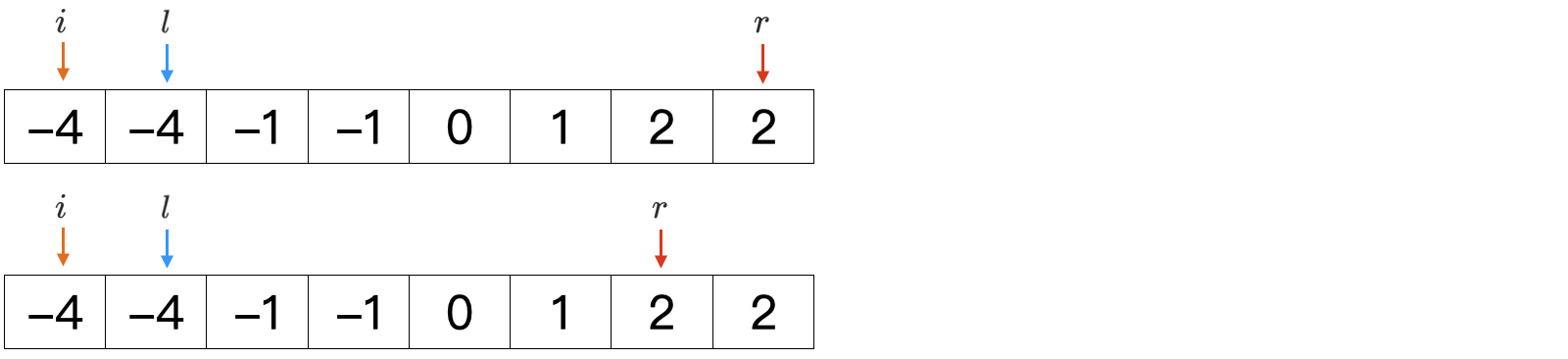
所以在移动指针的时候,需要规避连续的重复元素,比如下方的移动 r,对于 i,l 同理。
题目中要求不重复,所以从小到大枚举 i,l 的初值为 i+1,r 的初值一直为 num**s.size−1,分析同上。
下图为 i=1 的三指针初始位置。
复杂度分析
- 时间复杂度:O(N),双指针总计最多遍历整个数组一次。
- 空间复杂度:O(1),只需要额外的常数级别的空间。
